1. Binary Operation on Sets
The most basic set in esProc is sequence. Let's look at some basic
binary operations between two sequences A and B.
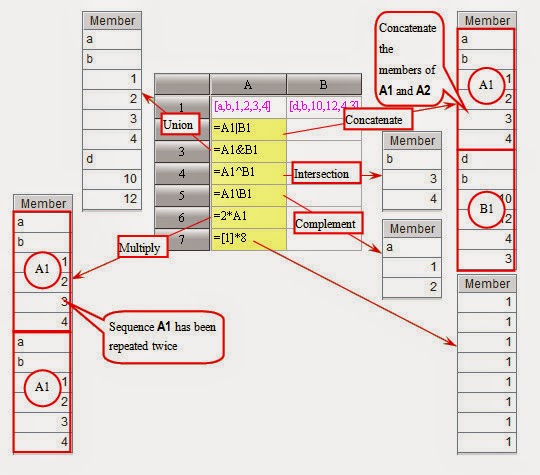
Ø A|B
Concatenate:
Concatenate the two sequence straightforwardly, of which the member of B is added behind the members of A. If A or B or both A and
B are the single-value member instead of sequence, then
it will be handled as a single member sequence.
Ø A&B
Union: Join the two
sets and remove the members of B that already exist in A. If one of A and B or
both vales are the single-value member instead of sequence, then you can take
it as single member sequence to process.
Ø A^B
Intersection:
Intersection set of A and B. Get
a sequence composed of members that not only exist in A
but also exist in B.
Ø A\B
Complement: Members
in A but not in B. If B is not a sequence, then treat it as the single member
sequence.
Ø k*A
A|A|…|A, copy A for k times, positions
of k and A are interchangeable in
the expression.
These basic operations - concatenate, complement, intersection and union - can also be used to deal with more complex set operations. Such as, to seek the “inverse intersection” of sets A and B, i.e., the set composed of all that is not the common members of A and B.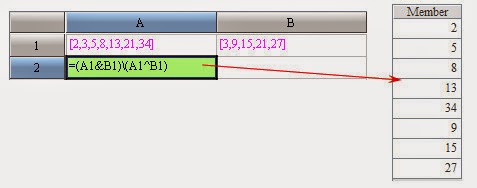
The "inverse intersection" of two sets is the complement of their union and intersection. With this kind of transformation, more complex binary operations will be completed.

These basic operations - concatenate, complement, intersection and union - can also be used to deal with more complex set operations. Such as, to seek the “inverse intersection” of sets A and B, i.e., the set composed of all that is not the common members of A and B.

The "inverse intersection" of two sets is the complement of their union and intersection. With this kind of transformation, more complex binary operations will be completed.
2 Alignment Arithmetic Operation on Sets
Two sequences which have the same length will perform the alignment computation on members, and return a new sequence.
Ø A++B
[A(1)+B(1),A(2)+B(2),…]
Ø A--B
[A(1)-B(1),A(2)-B(2),…]
Ø A**B
[A(1)*B(1),A(2)*B(2),…]
Ø A//B
[A(1)/B(1),A(2)/B(2),…]
Ø A%%B
[A(1)%B(1),A(2)%B(2),…],
the %
here is the Mod computation.
Ø A\\B
[A(1)\B(1),A(2)\B(2),…],
the slash here means integer division
3. Comparison of Sets
In esProc, the function cmp(A,B) can be used to compare the sequence A and B.
Ø cmp(A,B)
Compare the member
values of two sequences at the same location one by one, and return the 1 or -1 when encountering the
first unequal member, if A is identical to B, then return 0. Specifically, cmp(A) or cmp(A,0)
will compare A with the sequence with the same length
and members are all 0, i.e. cmp(A,[0,0,…,0]).
Comparison of two sequences can be briefly
expressed as A==B, A>B.
Note that a sequence in esProc is an ordered set, so
order plays an important role in comparing the size of two sequences A
and B. A.eq(B) is used to
see if the two sequences have common members.
Because the member order in A1 and A2 is different, result in A3 is
false, showing the two sequences are not equal. While result in A4 is true,
showing the two sequences have the same members.



没有评论:
发表评论